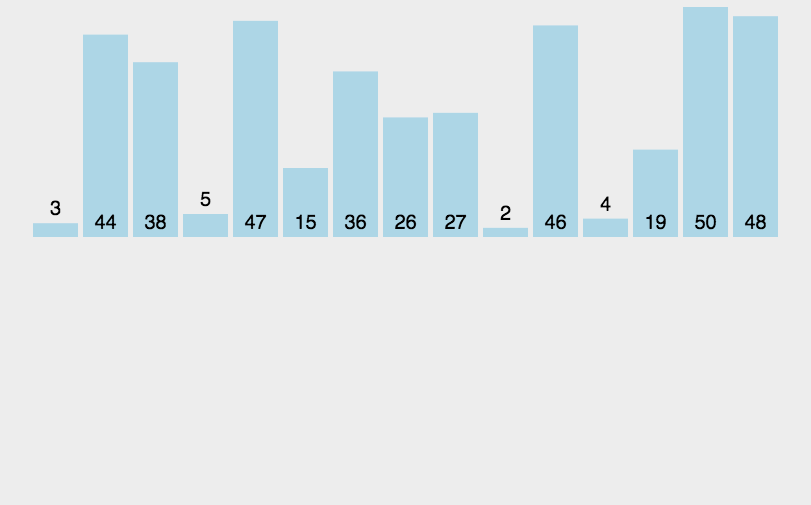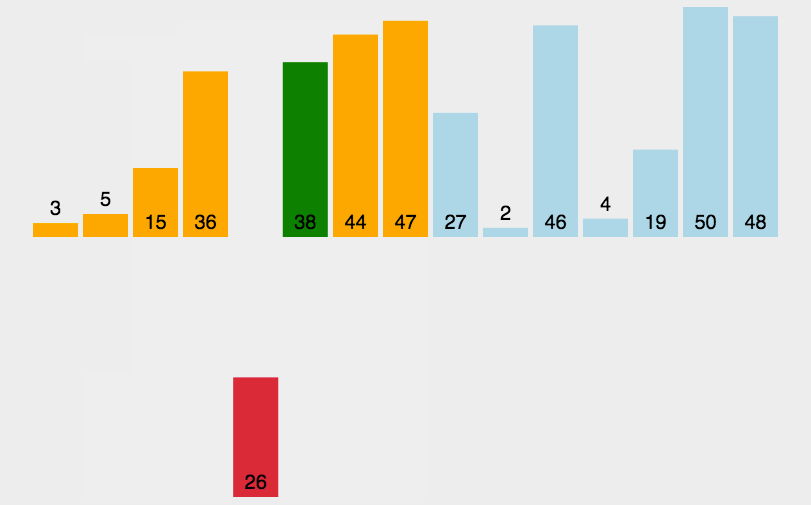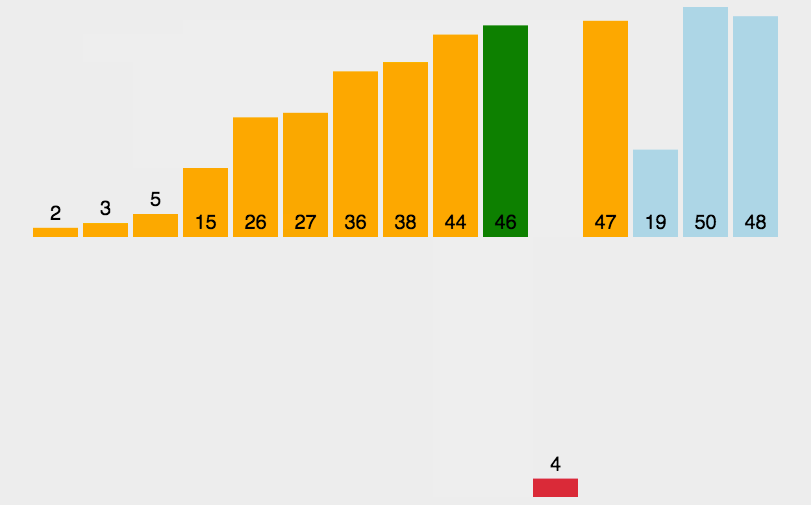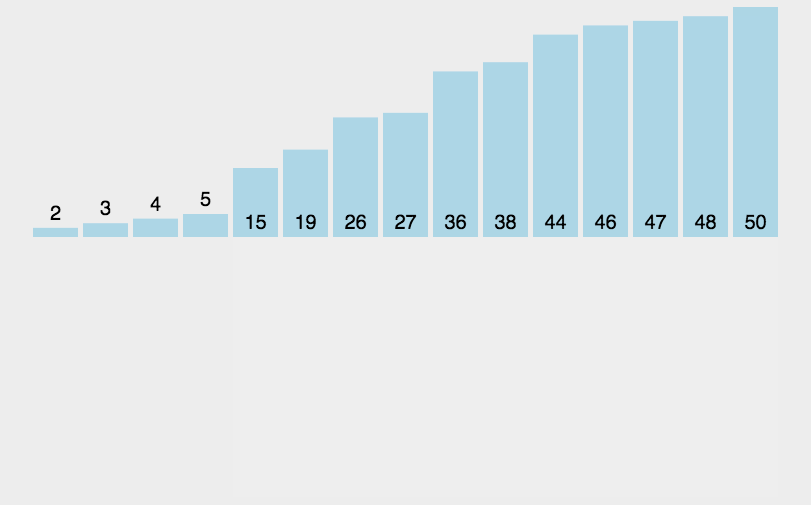
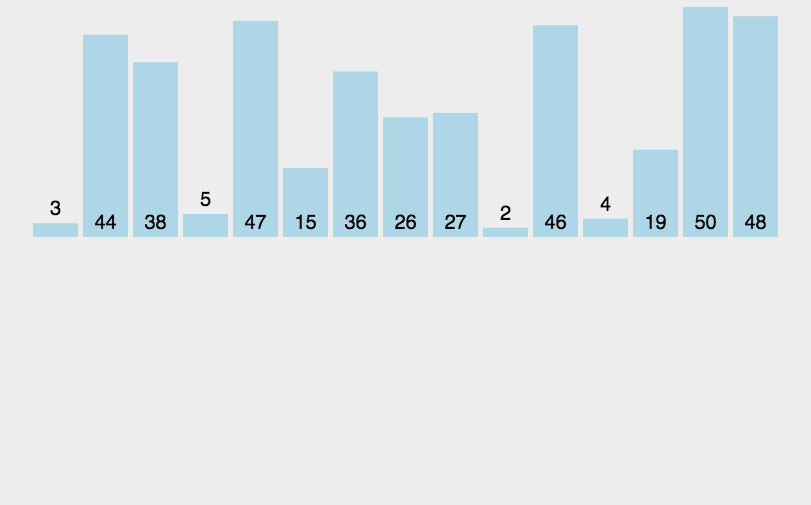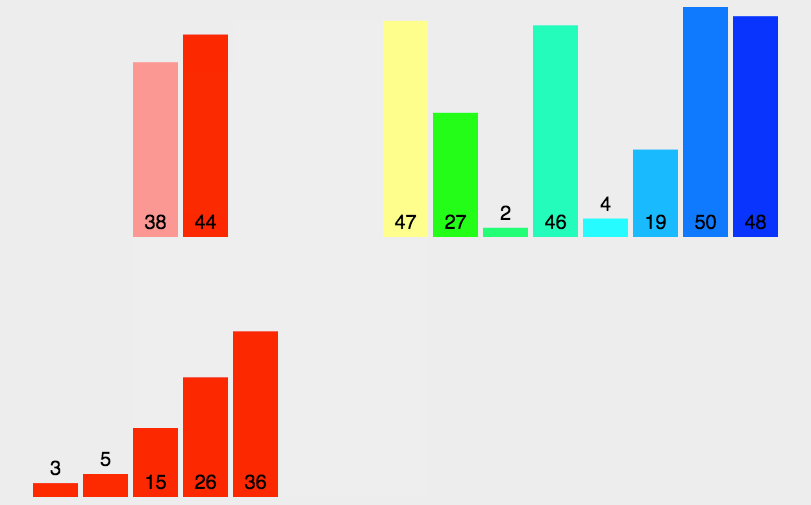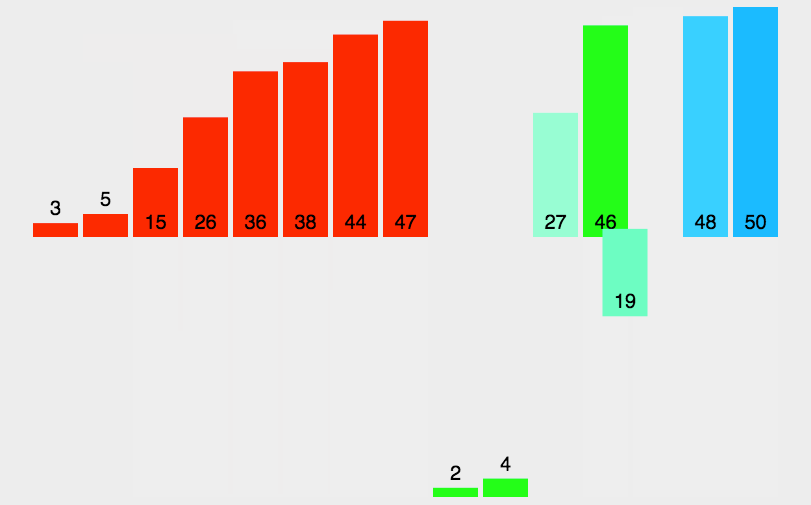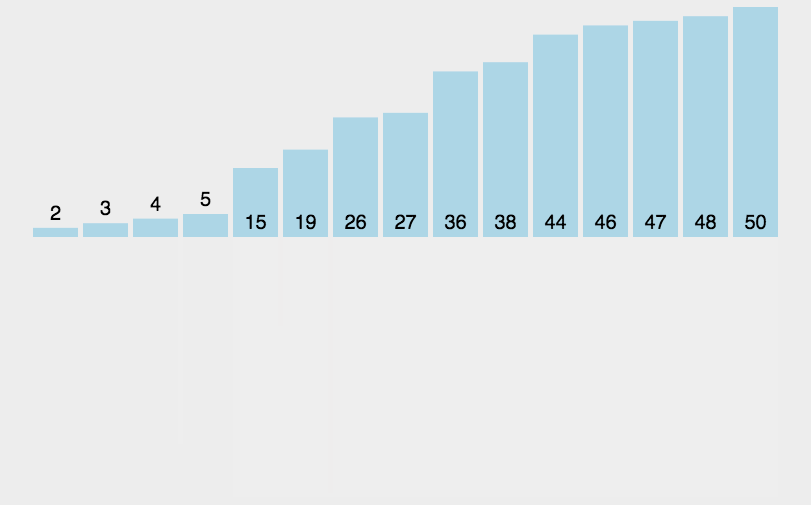
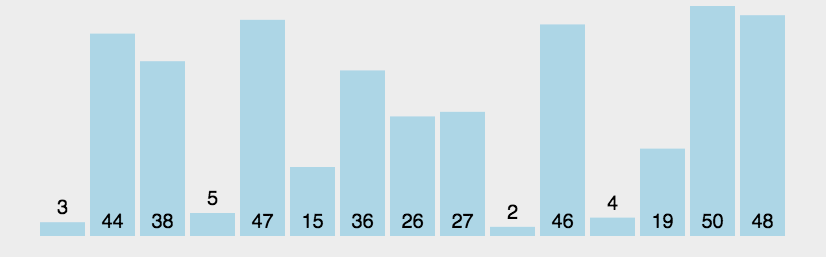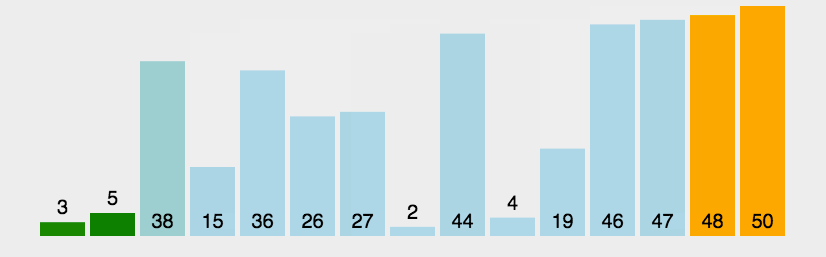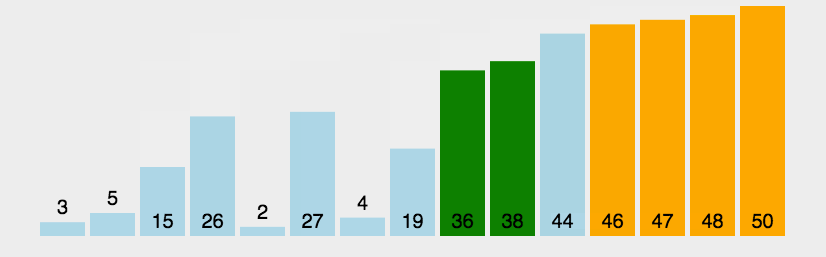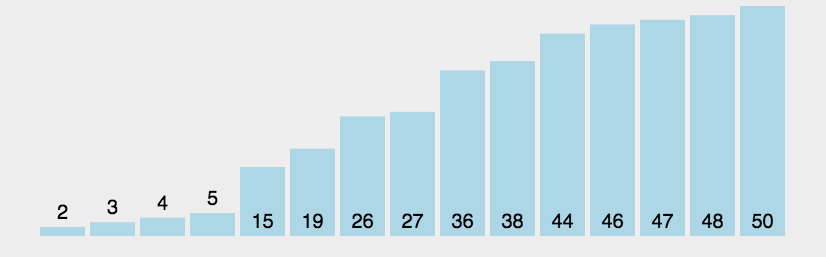各种排序的python实现
最近师兄师姐都在找工作,看到他们的笔试题中很多都是算法题。突然一个算法题摆在面前也是让人够懵逼的,于是我也复习一下各种排序算法吧,还是用python实现。
O(n^2)
平均时间复杂度均为O(n^2)的排序有三种:插入排序,选择排序和冒泡排序。这是三种比较简单的排序。
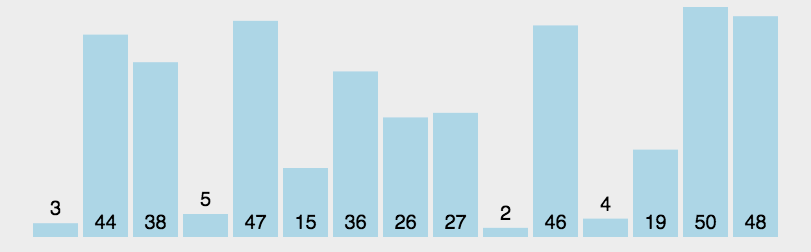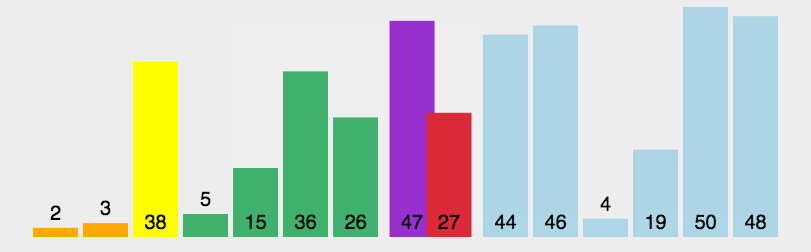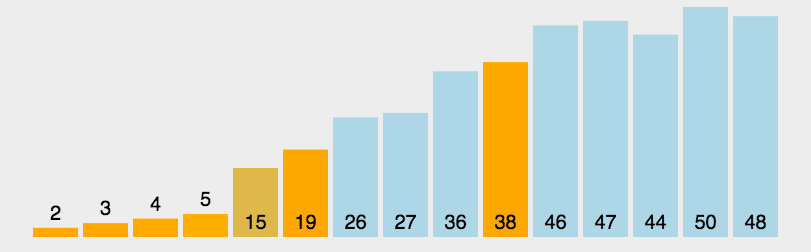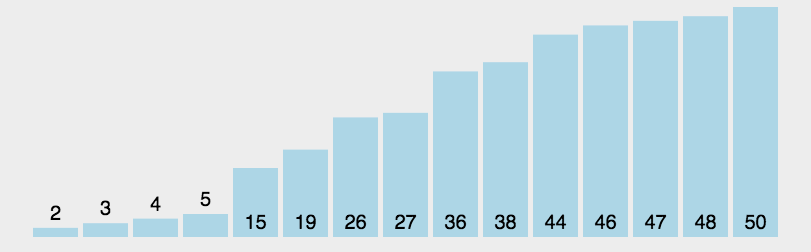
冒泡排序:
- 算法思路:每轮将最小(最大)的一个数交换到数组尾部(顶部)。
- 代码实现:
def bubble_sort(L):
length = len(L)
if length < 2:
return L
for i in range(length-1):
for j in range(length-i-1):
if L[j] < L[j+1]:
L[j], L[j+1] = L[j+1], L[j]
return L
- gif:
插入排序:
- 算法思路:每次提取一个数出来有序插入到它前面的数组。
- 将第i个元素提取出来与它前面部分的数组的元素一一比较,如果前面的数更大(更小),那么前面的数的序号+1.
- 当第i格元素不比它比较的数更大(更小)时,就把i元素放到它比较的元素后面。
- 当提取第i个数时,前面部分数组是有序的。
- 代码实现:
def insert_sort(L):
length = len(L)
if length < 2:
return L
for i in range(1,length):
key = L[i]
j = i-1
while j >= 0 and L[j] < key:
L[j+1] = L[j]
j -= 1
L[j+1] = key
return L
- gif
选择排序:
- 算法思路:每一轮标记出最小(最大)的数,然后把它放在有序位置上。
- 代码实现:
def select_sort(L):
length = len(L)
if length < 2:
return L
for i in range(length-1):
maxindex = i
for j in range(i,length):
if L[j] > L[maxindex]: # 找出最大数的索引
maxindex = j
if i != maxindex: # 把当前最大数放到当前循环队列首位
L[i], L[maxindex] = L[maxindex], L[i]
return L
- gif
O(nlogn)
平均时间复杂度为O(nlogn)的算法有:归并排序,堆排序和快速排序; 这些排序算法一般都需要进行迭代,可能需要多个函数,所以都写成可调用类的形式。
归并排序:
- 算法思路:
- 以单个元素为单位分组,然后两两排序,再将排好的序列递归地进行两两排序。
- 代码编写分为两个主要部分:先拆,后并。
- 对于一个子序列,分成两份,比较两份的第一个元素,小者弹出,然后重复这个过程。对于待排序列,以中间值分成左右两个序列,然后对于各子序列再递归调用。
- 代码实现:
class merge_sort(object):
def _merge(self, alist, p, q, r):
left = alist[p: q+1]
right = alist[q+1: r+1]
for i in range(p, r+1):
if len(left) > 0 and len(right) > 0:
if left[0] > right[0]:
alist[i] = left.pop(0)
else:
alist[i] = right.pop(0)
elif len(right) == 0:
alist[i] = left.pop(0)
elif len(left) == 0:
alist[i] = right.pop(0)
def _merge_sort(self, alist, p, r):
if p < r:
q = int((p+r)/2)
self._merge_sort(alist, p, q) #先拆左边,拆到单个元素为止
self._merge_sort(alist, q+1, r) #拆分合并过程类似二叉树结果
self._merge(alist, p, q, r)
def __call__(self, sort_list): #让merge_sort成为callable类,即可调用
self._merge_sort(sort_list, 0, len(sort_list)-1)
return sort_list
- gif
堆排序:
- 算法思路:
- 堆结构类似二叉树,以列表形式存储。i节点的子节点是i*2+1和i*2+2,二叉树的前n/2个节点是非叶子结点。
- 堆排序就是迭代创建最大值堆的过程:
- 建立最大值堆,把最大值与最尾节点交换。
- 将最尾元素之前的列表进行建堆(之前行为只改变了堆顶节点,所以这时只需要对堆顶节点建堆),并把最大值与此时列表最尾节点交换,迭代这一过程。
- 代码结构:
- 针对某一节点的建堆函数:比较某一节点与其子节点的值,交换出最大值,并对这一 节点的子节点迭代调用此函数。确保以某一节点为堆顶的堆是最大值堆。
- 对所有非叶子结点从下往上迭代建最大值堆,确保整个堆是最大值堆。
- 将堆顶节点交换到堆尾,并对其余节点迭代此过程。
- 代码实现:
class heap_sort(object):
def _left(self, i):
return 2 * i + 1
def _right(self, i):
return 2 * i + 2
def _max_heapify(self, alist, i, heap_size=None):
"""
从某个节点开始构建最大值堆,并迭代
"""
length = len(alist)
if heap_size is None:
heap_size = length
l = self._left(i)
r = self._right(i)
if l < heap_size and alist[l] > alist[i]: # 确保子节点存在
max_index = l
else:
max_index = i
if r < heap_size and alist[r] > alist[max_index]:
max_index = r
if max_index != i:
alist[i], alist[max_index] = alist[max_index], alist[i]
self._max_heapify(alist, max_index, heap_size) # 这里要迭代是为了保证堆是最大值堆,既每个父节点都大于子节点
def _build_max_heap(self, alist):
rood_end = len(alist) / 2 # 获取到所有非叶子节点
for i in range(rood_end)[::-1]: # 从非叶子结点开始构建最大值堆
self._max_heapify(alist, i)
def __call__(self, sort_list):
self._build_max_heap(sort_list)
heap_size = len(sort_list)
for i in range(1, heap_size)[::-1]:
sort_list[0], sort_list[i] = sort_list[i], sort_list[0]
heap_size -= 1
self._max_heapify(sort_list, 0, heap_size) # 最大值堆已建好,这时只需要针对堆顶建堆
return sort_list
- gif
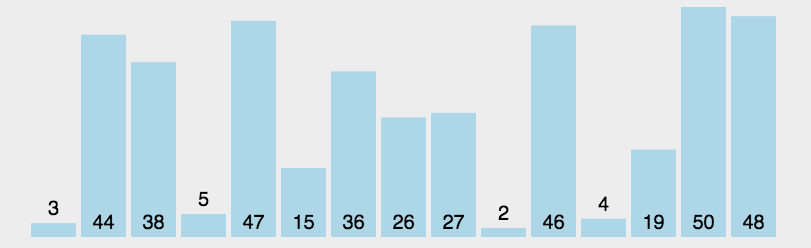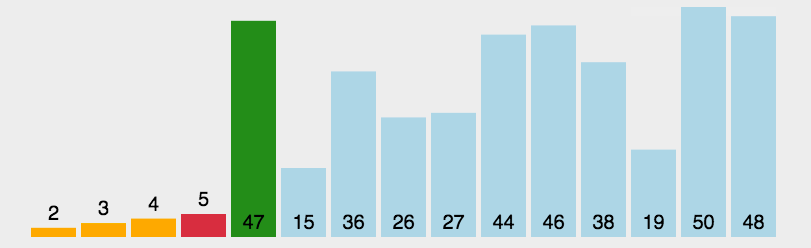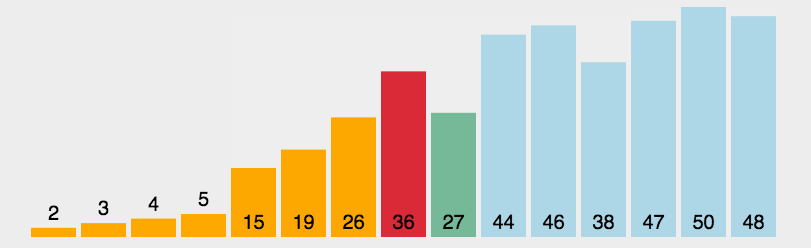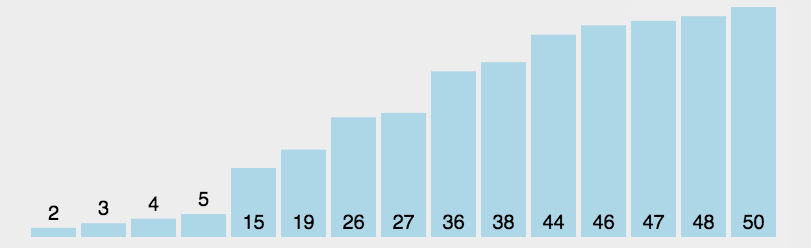
快速排序:
- 算法思路:
- 选取一个基准值,大于基准值的数放左边,小于基准值的数放右边(类似于二叉查找树)。再对每个子序列迭代这一过程,直到子序列为单个数。
- 对于一个已知基准值的列表,如何将比基准值大的数放到基准值右边,比基准值小的数放基准值左边?
- 设置一个指针,使指针右边的数都是比基准值大(也就是说,指针指向的是最后一个比基准值小的数);
- 循环列表时,如果遇到比基准值大的数,指针位置不变;如果遇到比基准值小的数,指针向后移,并且将这个数与此时指针指向的数(第一个比基准值大的数)交换位置,使指针指向的又是最后一个比基准值小的数;
- 循环完成之后,将基准值与指针后的第一个数(第一个比基准值大的数)交换位置,这时基准值左边的数都比它小,右边的数都比它大。
- 代码实现
import random
class quick_sort(object):
def _partition(self, alist, p, r):
i = p-1 # 设置指针,首先假设所有数都比基准值大
flag = random.randint(p, r) # 随机选取基准值
x = alist[flag]
alist[r], alist[flag] = alist[flag], alist[r] # 将基准值放到列表最后方,方便循环处理
for j in range(p, r): # 对于基准值之前的数进行循环
if alist[j]<x:
i += 1
alist[i], alist[j] = alist[j], alist[i]
alist[i+1], alist[r] = alist[r], alist[i+1]
return i+1 # 返回的是基准值的index
def _quicksort(self, alist, p, r):
if p<r:
q = self._partition(alist, p, r)
self._quicksort(alist, p, q-1) # 迭代基准值之前的序列
self._quicksort(alist, q+1, r) # 迭代基准值之后的序列
def __call__(self, sort_list):
self._quicksort(sort_list, 0, len(sort_list)-1)
return sort_list
- gif
Comments